统计功效是什么
通过前面的文章,我们已经了解,A/B实验背后的统计学模型是(双样本)假设检验。同时,由于实验时存在抽样误差,我们的实验总会“犯错”。而统计学可以告诉我们,我们可能会犯什么错,以及有多大几率犯错。
假设检验过程中,我们可能犯的两种错误分别是:第一类错误(弃真)、第二类错误(取伪)。
第一类错误 的表现是: 我的策略其实没用,但是实验结果却显示我的策略有用 。显著性水平刻画了实验者出现此类错误的概率,即在原假设正确的前提下拒绝原假设的概率。
在实验中,我们也可能会出现另一种情况: 我的策略其实有用,但是我没有检测出来 。这便是统计学中 第二类错误 的表现。也就是说,在原假设是错误的前提下,实验者也可能会接受原假设,这在统计学中被称为第二类错误。这种错误的概率被记为 β。 而统计功效(power,也被称为检验效力),被定义为1- β ,表示的是“ 假设我的新策略是有效的,我有多大概率在实验中检测出来 。”
统计功效的理论依据
现在我们举个例子,尽可能直白地解释一下统计功效到底是怎么一回事。
PS:如果认为理论部分过于难理解,也可以选择直接越过此小节,阅读后面的实操部分。
假设现在我们要进行一组实验,我们认为:将旧策略A调整至新策略B,能够将用户的人均观看时长提升3%。从假设检验的角度去分析我们要进行的实验可以得出,在这组实验中:
原假设=新策略B没用
备择假设=新策略B有用
同时,通过前面的学习我们也了解到:实验中我们不断抽样所得出的样本均值,大致会呈现正态分布。接下来看看下面这张图。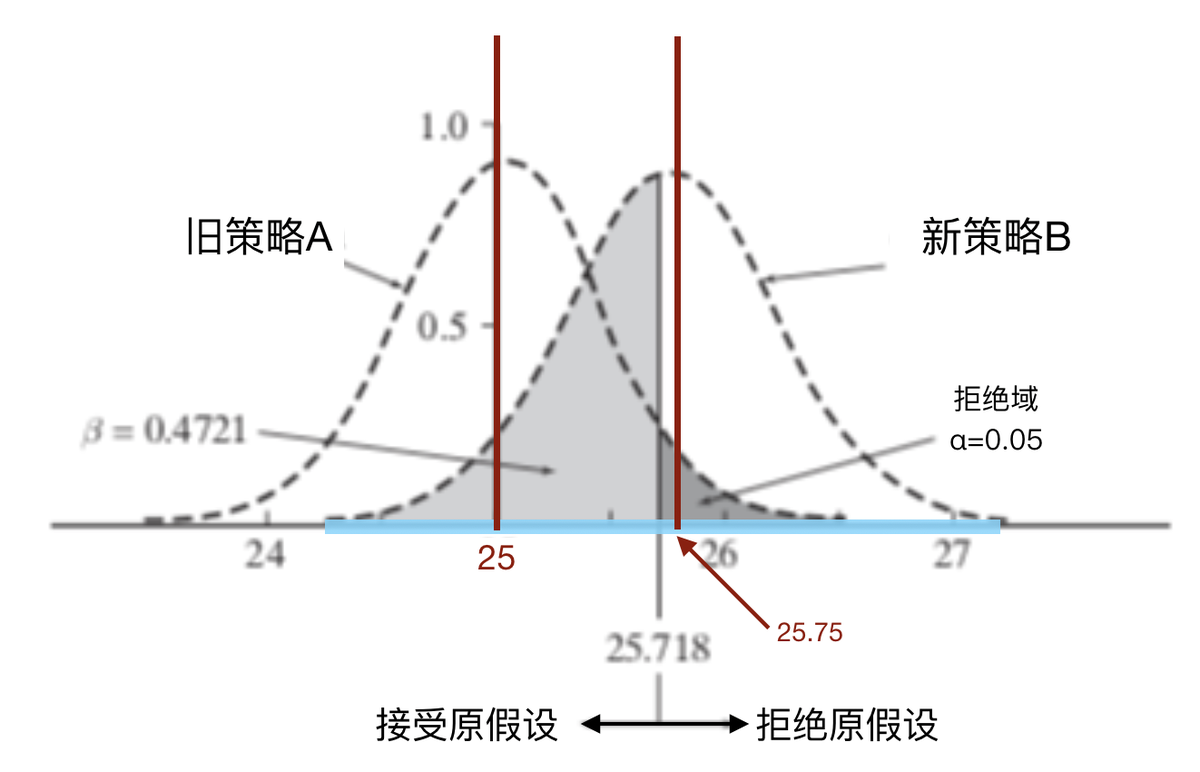
图中,左侧钟形曲线代表原假设成立时,经抽样统计,平均阅读数所呈现出的分布形态。这条曲线对应的策略实际上是“旧策略A”。假设旧策略A生效时,用户平均阅读数的真值为25s(意味着钟形曲线的中轴线在横轴上对应的值是25);且在这一分布中,当平均阅读数均值超过25.718s时,我们会拒绝原假设,认为新策略B有效。那么。从图中来看,深灰色区域即拒绝域。
说完了左边的,我们再来看看右边的。右边钟形曲线对应的策略是新策略B。我们现在假设这一策略生效时,用户的人均观看时长真值是25.75s(即右侧钟形曲线的中轴线,在横轴上对应的值是25.75)。
先来想一下,右边钟形曲线的真值为25.75,落在旧策略A的拒绝域里,这意味着什么呢?这意味着, 理想状态下,新策略B其实是有效的 。但是,通过前面文章的学习,我们也知道,在对新策略B做抽样统计时,由于抽样误差,我们得到的平均阅读数均值大概率不会是25.75。看到图中横轴上的蓝色区域了吗?如果对新策略B做抽样统计时,其平均阅读数均值可能是蓝色区域内的任意一个数字。
- 假如在统计时,新策略B的样本均值,落在原策略A的拒绝域之中或者拒绝域右侧。此时我们可以得出结论:拒绝原假设,新策略B是有用的。
- 假如新策略B的样本均值<25.718,对应上图,此时样本均值落在图中浅灰色的范围内。此时,由于样本均值并不在原策略A的拒绝域之中,所以我们没办法拒绝原假设,也就无法证明新策略B是有用的。
我们在前面已经讲到过,新策略B在抽样检验中,它的真值实际落在原策略A的拒绝域里。理论上来说,新策略B实际上是有效的。但是,如果新策略B进行抽样统计后,样本均值<25.718,我们便无法出检验出新策略B有效。这就犯了我们所说的 第二类错误 :“ 我的策略其实有效,但是我没检验出来 。”
在上面的图中,浅灰色区域就是我们犯第二类错误的域,其面积占右侧钟形图形面积的比率,就是我们犯第二类错误的概率。这一概率被记作 β 。在图中的例子里, β 的取值为47%(计算过程就不展示了)。也就是说,在上面的例子里,即便我的新策略B有效,我仍有47%的概率没法检验出它是有效的。而统计效力=1- β =53%。这代表着我有53%的概率可以检测出新策略B是有效的。
统计功效在A/B测试中的使用
相对于显著性水平来说,统计效力更难让人理解。为了让大家在实验中更方便地应用统计功效,A/B测试平台引入了一个额外参数:检验灵敏度(MDE)。“检验灵敏度”,指我们所关心的指标,在实验中可检测出来的最小提升值。这个提升值越小,也就意味着检验越灵敏。
灵敏度来和统计效力有什么关联呢?抛开理论知识,从直觉上来看,A/B实验应该遵从以下两个事实:
- 新策略的效果越大,越容易被检验出来;
- 样本的数量越多,检验能力越强,越能分辨新旧策略间细小的不同。
换句话说:
- 新策略的效果越大,检验所需的灵敏度越低(意味着检验灵敏度的取值更大。灵敏度10%和灵敏度1%相比,10%灵敏度低),同时实验结果出现显著的概率越高,实验的统计效力也就越大;
- 实验调用的样本数量越多,其灵敏度也就越高。
那么,在实际的实验操作中,灵敏度(或者说统计效力)有什么应用场景呢?
No.1 实验不显著,要不要结束实验
这几乎是每个实验操作者都会遇到的问题:辛辛苦苦做了个实验,数据是涨了一点,但是实验结果不显著。咋办?现在把实验停了,换新的思路?还是让实验再跑一段时间,这会不会影响实验结果的可信性,在这个问题上,“灵敏度”就能帮你了。
注意
灵敏度会随实验的样本量增加、运行时长增长而越来越灵敏(灵敏度数值越来越小)。理论上,只要你的A/B实验跑的时间足够长,样本足够多,实验总会显著的。
当实验结果不显著时,实验者可以在实验报告中查看当前实验中,我们所关注的指标的MDE是多少,并判断灵敏度是否大于指标的预期提升值。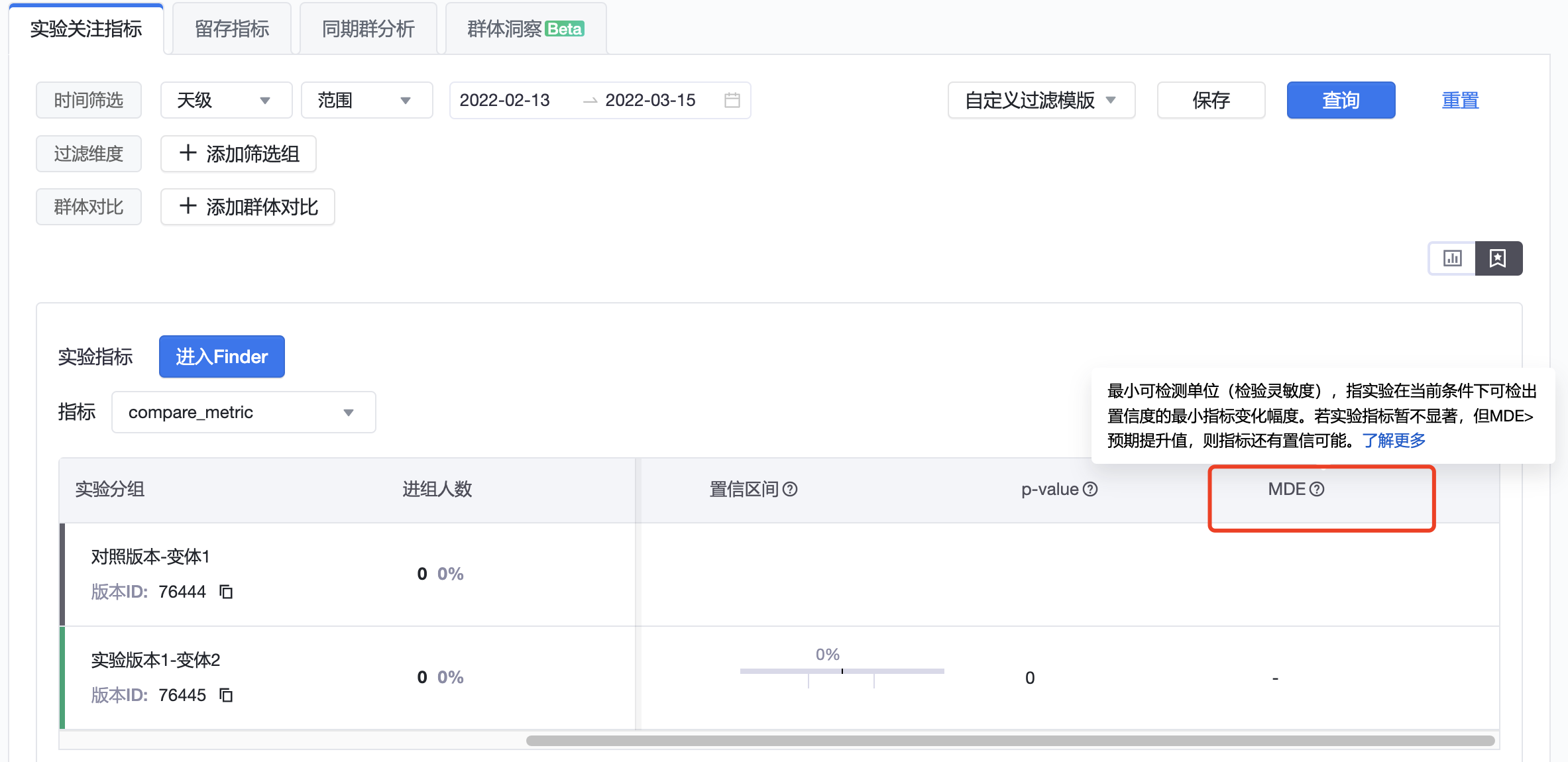
如果指标的灵敏度比预期提升值大,那么我们可以将实验延长几天,再观察一段时间;如果灵敏度已经比预期提升值小了,那么很遗憾,我们的实验结果没有置信的可能了,另起炉灶吧。
为什么要这样做呢?我们举个例子。如果在一个实验中,我期望我的新策略将平均阅读数提升3%。经过一段时间的实验后,我发现新策略下平均阅读数提升了2.5%(虽然没有预期中好,但也不错),实验结果不置信。按图索骥,此时我们应该查看平均阅读数这一指标的检验灵敏度:
- 如果灵敏度>3%,意味着可能你的实验可能会有3%的显著提升,只是灵敏度还不够,我们还没检验出来。所以我们可以再将实验延长一段,让更多样本进入实验,使得实验更灵敏;
- 如果灵敏度<3%,意味着现在的灵敏度已经足够检测出3%的显著提升了。但是现在你的实验还是不显著,那么也许是你的策略真的没那么有用。我们该再选个新策略了。
No.2 实验还没开,到底要多少流量
前面的例子里,当一定流量进入实验后,我们可以了解到实验的灵敏度。反过来讲,如果用户愿意指定自己需要的灵敏度,A/B测试同样可以推算出实验需要多少流量。
使用这一功能的操作也很简单。在新建实验第四步-“设置目标受众”时,在“流量分配”的步骤中,可以点击“算一算开多少流量合适?”,进入到实验流量建议工具,输入相关信息后,A/B测试就可以轻松计算出,实验总共需要多少流量。
「如何确定灵敏度MDE大小」
在这里我们也会面临一些问题:我怎么确定自己需要多大的灵敏度呢?其实这相当于,我们需要知道:在目前的实验策略下,我所关注的指标最低提升百分之多少,我才能够接受。
如果我们想上线(全量发布)一个新策略,我们需要考虑到开发成本、上线成本、潜在风险等等问题。这时我们需要从产品层面去思考:指标要提升多少,才能覆盖我上线这个新策略所要付出的成本。假如我认为:“新策略至少要让人均阅读数指标提升1%,否则新策略就不值得全量上线。”那么,我们预期提升值的最低值就是1%,我们在实验中所需的灵敏度也应当是1%。
在实验前,我们必须明确自己的实验目的、具体的指标,以及指标预期的提升值是什么。灵敏度,应该与我们指标预期的最低提升值相同。
「灵敏度不可过高/过低」
同时,我们也需要指出,灵敏度太高或者太低,都有其弊端(也可以理解为,指标的预期提升值定的太高或太低都不好)。
- 灵敏度太低(MDE取值过大)
过低的灵敏度(比如理论上指标提升1%收益就很大了,但我们却将灵敏度设置为5%),可能导致我们与有潜力的策略失之交臂。
- 灵敏度太高(MDE取值过小)
设置过高的灵敏度,一方面会导致调用过多流量,形成不必要的流量浪费;另一方面,过大的流量往往会使指标更轻易地形成显著,但其实这种显著并没有实际意义。
还记得我们前面说的吗,理论上来说,只要样本足够多(比如无穷多时),实验组和对照组之间任何一点差异都会形成统计显著。这就像是一个哲学问题,策略A和策略B,无论他们多相像,但终归是不一样的,终归会造成实验结果的差异。但这种差异的显著有意义吗?比如新策略使指标提升0.001%,且统计显著,这真的有意义吗?
综上,灵敏度的选择,要结合每个实验场景的实际情况,慎重判断。