You need to enable JavaScript to run this app.
导航
A/B测试（DataTester）私有化
  • 文档首页
    • /A/B测试（DataTester）私有化/功能指南/查看与分析实验报告/实验报告概述
实验报告概述
最近更新时间：2024.06.05 10:36:45首次发布时间：2023.09.14 11:50:10
我的收藏

一. 术语表
  • 差异绝对值：当前实验版本相对于对照版本的绝对差异。
  • 差异相对值：当前实验版本相对于对照版本的绝对差异/基准版本值。
  • p-value：在原假设为真的前提下随机抽取样本出现极端情况的概率。当p-value<1-置信度水平，认为统计显著。
  • 置信区间：由样本统计量构造的总体参数的估计区间。
  • MDE：Minimum Detectable Effect最小可检测单位(检验灵敏度)，当前条件下能有效检出指标置信度的diff幅度。
  • 概率密度：probability density，也有称为概率分布曲线（Probability Curve）。以概率密度为纵坐标，区间为横坐标，概率密度对区间的积分就是面积，该面积就是事件在这个区间发生的概率，所有面积的和为1。

二. 实验报告

「A/B测试」的实验报告模块，基于假设检验理论针对实验结果对比、提供结论性的推断。报告概览的进组用户数据为次日T+1数据，即1号的进组用户数据将在2号展示在报告概览中。如下：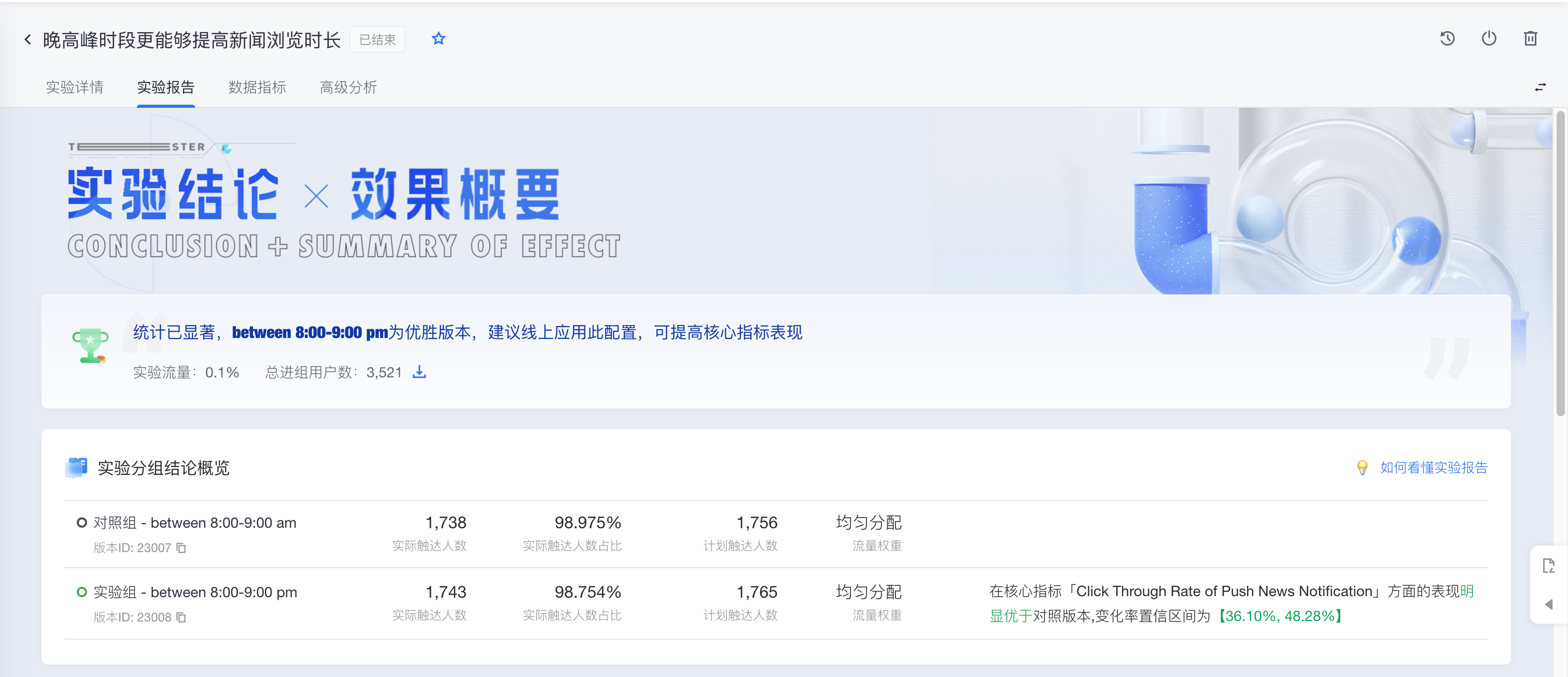
图片
实验报告页面除了展示实验的基本结论外，还包含核心指标的具体表现以及对应的天级趋势图、概率分布图和箱型图（原盒须快照）
图片

三. 数据指标

数据指标包含事件指标、留存指标以及漏斗指标三个大类

3.1 事件指标

3.1.1 指标导航

实验数据左侧指标导航将会分组展示本实验的所有「关注指标组」，推荐将一组关联使用的指标放在一个指标组中。默认展示「核心指标」所在的指标组，在导航选中某指标后，右侧视图会自动锚定至该指标组-指标所在位置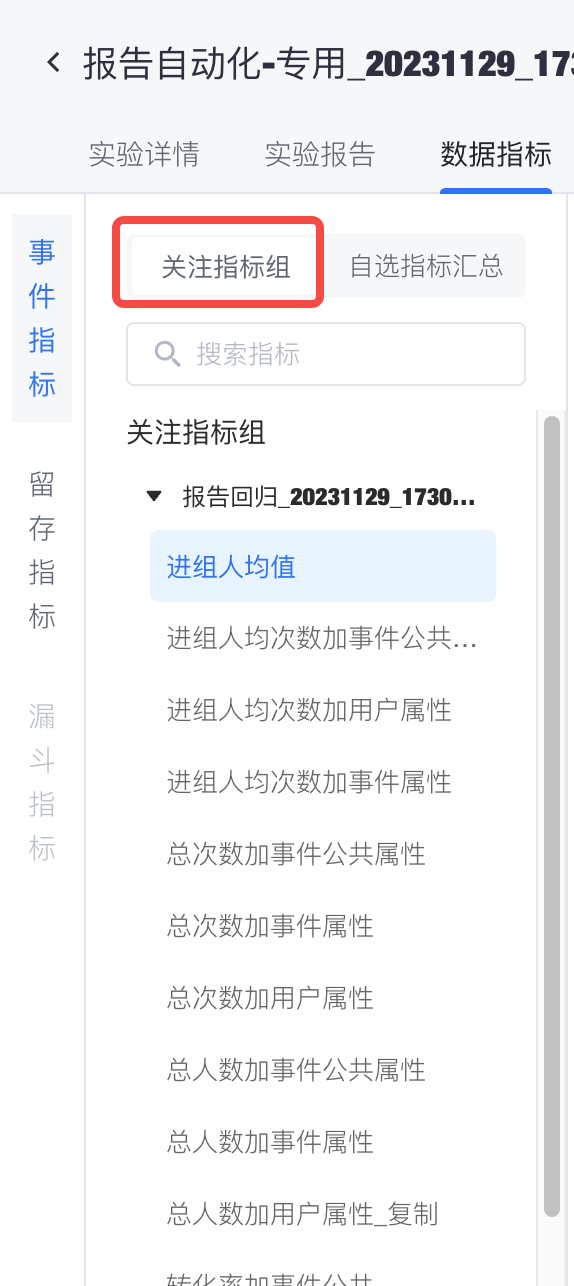
图片

3.1.2 指标信息

  • 默认视图为「指标组视图」，支持切换为「指标视图」
  • 表格中每个指标依次展示了「差异相对值」、「置信区间」、「指标值」，同时用颜色标记Diff的显著性检验结果
  • hover数据表格，会展示指标表现的详细解读

图片

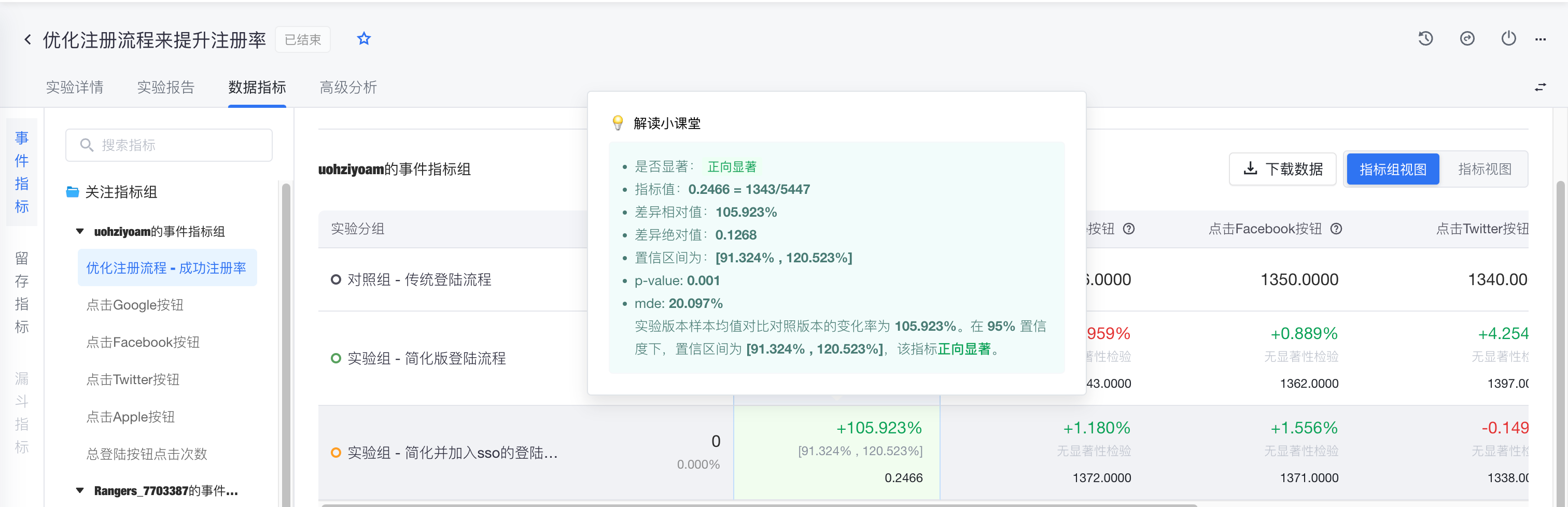
  • 单指标视图展示版本进组人数、指标值、实验版本相对指标的diff值以及相对变化和置信区间等信息，并支持查看天级趋势、概率分布和箱型图

图片

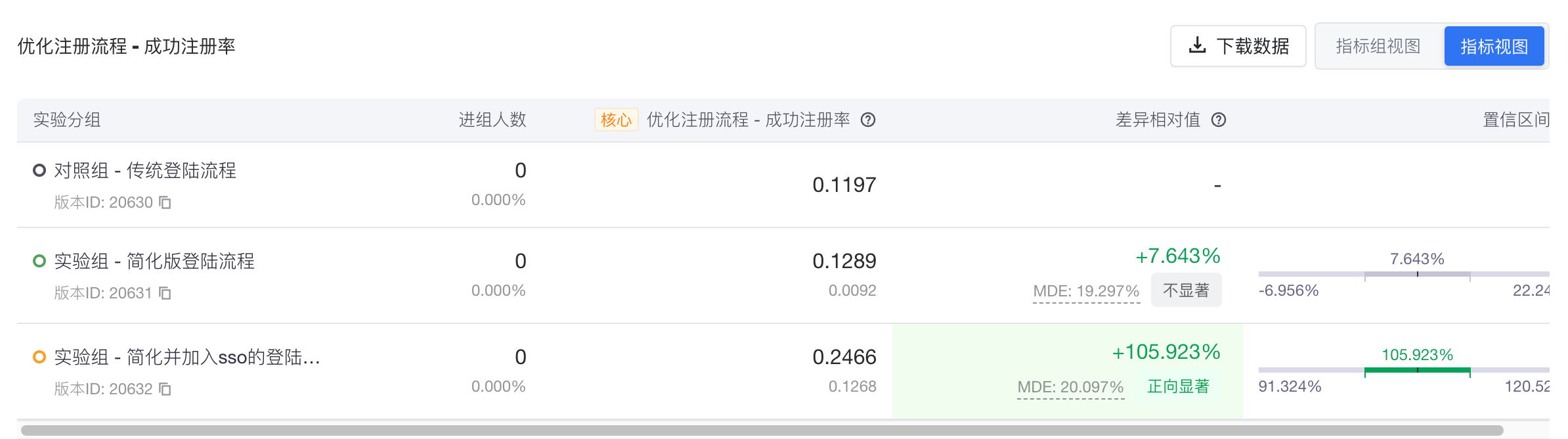
3.1.3 添加过滤条件

  • 支持添加时间、维度的过滤条件。如下：

图片
其它相关信息说明：

  • 天级不包含今日，切换到小时、分钟级可以看到今日的数据。
  • 创建实验当天，在「实验关注指标」默认显示实时数据（5分钟级）。结束实验当天，即使实验已结束，您仍然可以查看实时数据。
  • 若实验开启日=实验结束日，实验结束后，「关注实验指标」默认为实时数据颗粒度（5分钟级）。当实验开启日≠实验结束日时，实验结束当日，「关注实验指标」默认为天级颗粒度。

3.1.4 时间趋势

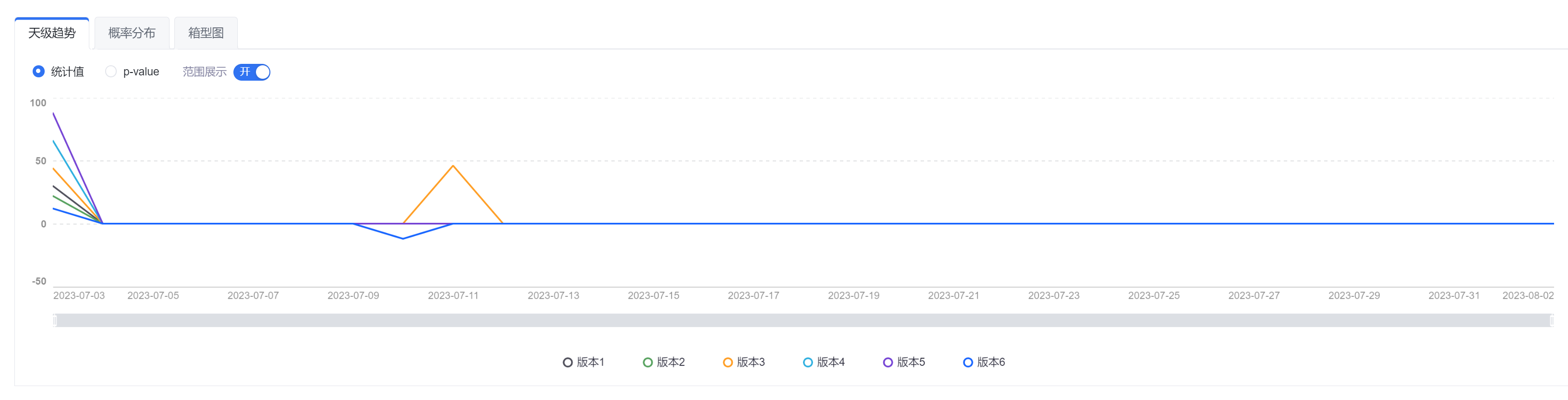
根据实验报告的时间颗粒度，展示某个指标的「天级趋势」、「时级趋势」、「分钟趋势」。 以「天级趋势」举例：

  • 可查看当日指标的统计值和p-value，以及当日统计值的范围。日均定义口径为当前所有已经进组的用户在当日的指标表现，并非当日新进组用户。
  • 当打开「范围展示」，出现范围，会产出重叠效果，并查看各个版本的核心指标范围随时间变化的情况。
    • 理想情况下，范围会随着时间而变小，并且在图中反映出来。
    • 如果范围扩大，则表明数据波动。
    • 如果范围重叠，则表示不确定哪个版本效果更好。
      图片

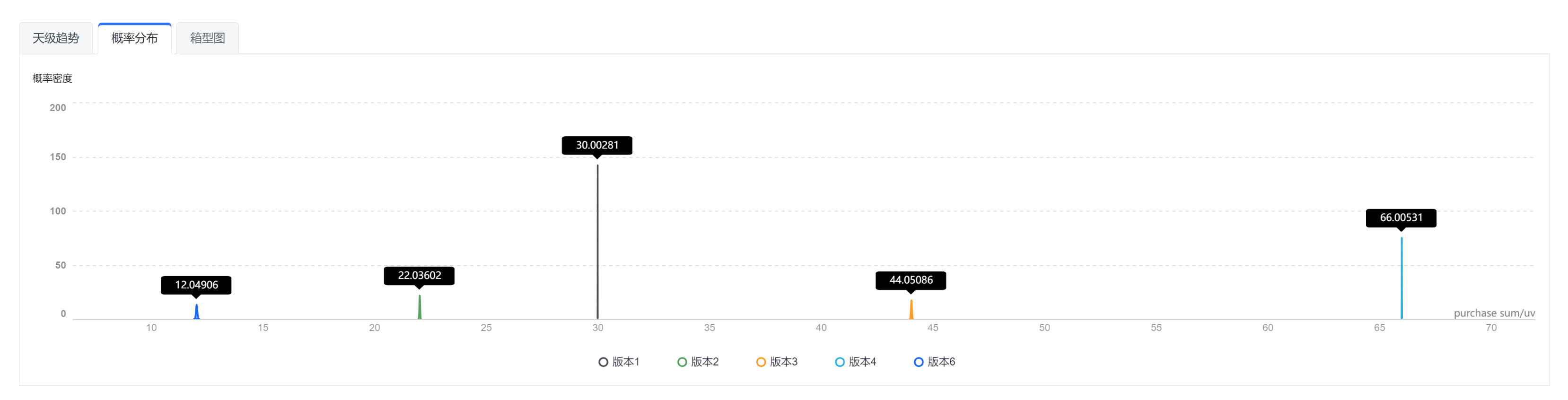
3.1.5 概率分布

概率分布，展示的是指标的取值及其出现的概率分布，横轴是指标值，纵轴是指标值出现的概率密度，通过均值和方差反映指标的分布情况。实验组和对照组的概率分布对比，可辅助判断实验组和对照组的差异情况。

  • 默认对照版本采用灰色系，其他版本采用彩色系。
  • 在不同实验版本的正态分布曲线上，鼠标hover会显示各个版本的“进组人数、p-value、指标方差、MDE、置信区间”信息。

图片

3.1.6 箱型图

盒须快照，又称为箱型图，是通过数据的最大值、最小值、中位数和两个四分位数，反映原始数据分布特征。通过实验组和对照组的盒须快照对比，可以进行两组数据分布特征的比较。
应用说明：

  • 针对人均类型（PV/AU、PV/UV、SUM/AU、SUM/UV）、PV类型、SUM类型、CTR点击率类型、PV/SUM & SUM/PV & SUM/SUM & PV/PV等类型指标均可适用。
  • 「CVR转化率类型」因对单个个体是二元值，目前不支持盒须图。
  • 小时级/分钟级的粒度展示，不提供盒须图。

重叠区域说明：各颜色的阴影区域为对应实验组和基准组的重叠区域，重叠区域表示不确定哪种版本效果更佳。如果您表现最好的版本有很多不确定性重叠，我们建议您将实验运行时间调的更长。
图片

3.1.7 自选指标视图

新增「自选指标汇总」视图，来支持跨指标组的指标汇总展示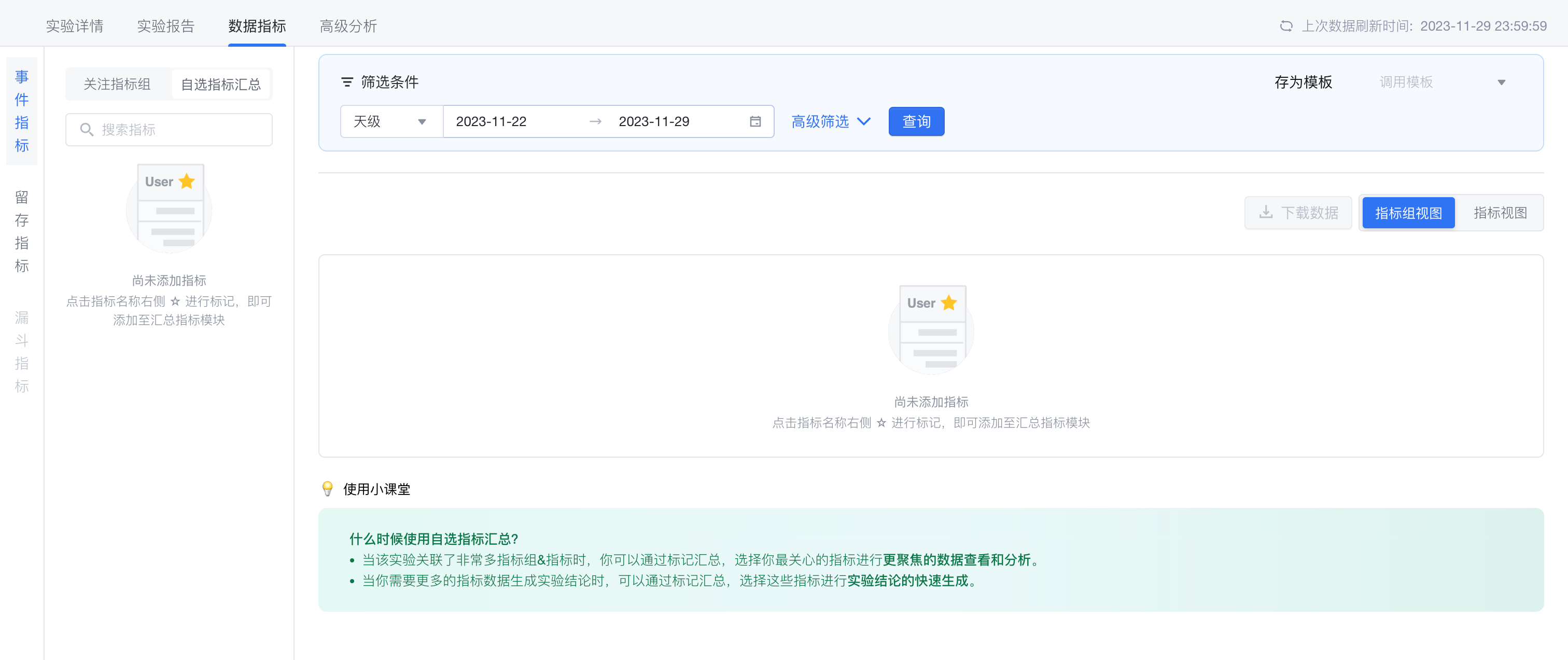
图片

  • 在「关注指标组」中标记指标，即可添加至「自选指标汇总」中

图片
图片

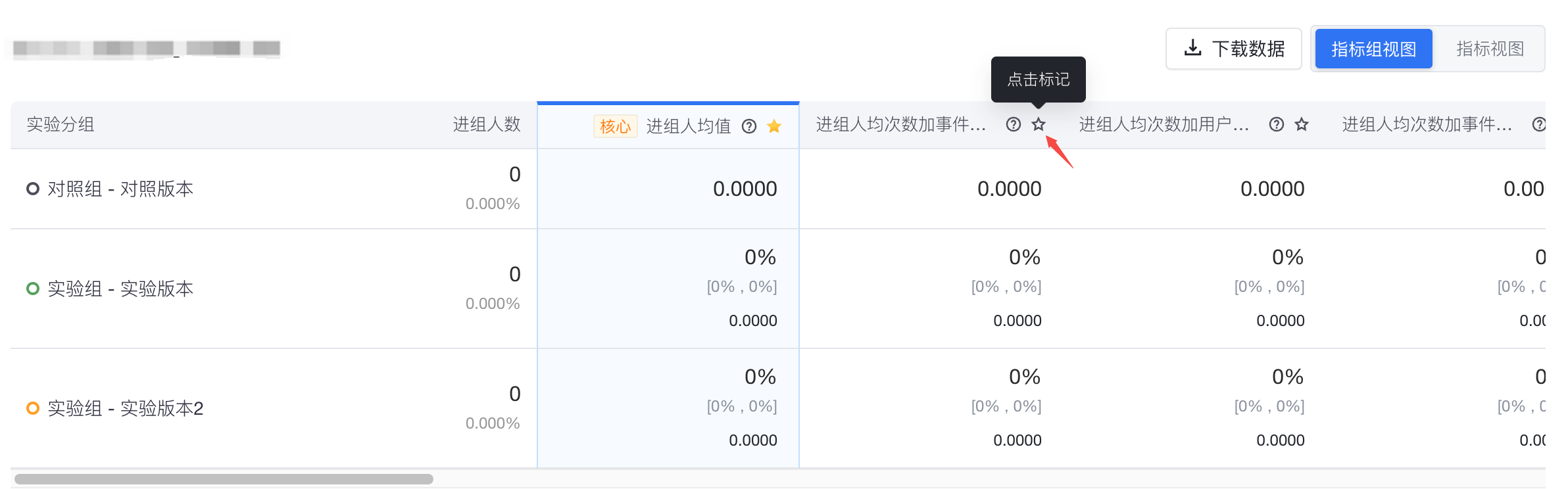
3.2 留存指标

3.2.1 同期群留存趋势**

同期群留存趋势，指的是将实验用户以首次进入实验的日期拆分，观察不同天首次进组的用户在后续的留存趋势。 支持细分群组的累计趋势图，支持1日留存率至30日留存率的天级趋势图。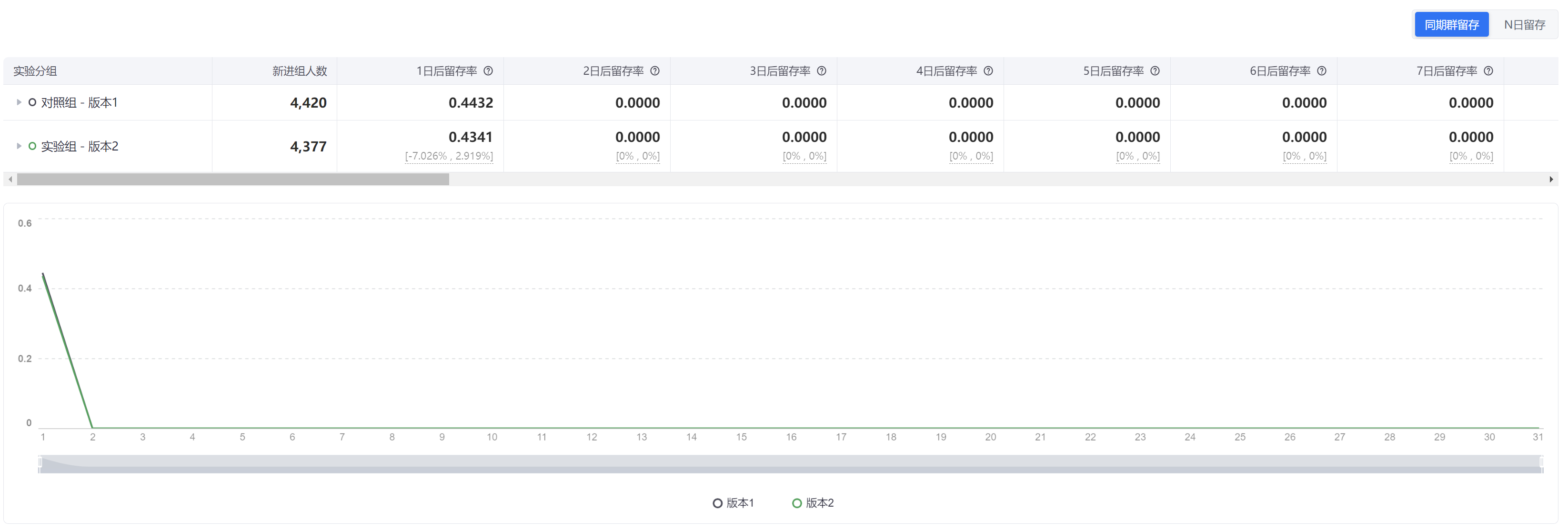
图片

3.2.2 N日留存日趋势

表示筛选时间范围内进组用户的第N日留存趋势。
图片
留存率是系统默认配置的，如何计算留存率？

规则

处理逻辑

分组方式

首次进入实验组的用户（不一定是新用户）

归因方式

把留存用户按照进组时间划分，分别归因到首次进组的时间

回访规则

回到APP即视为回访

举个例子说明：

  • 第一天实验组A的用户数为：10000，第一天base_user为10000；
  • 第二天实验组A的用户数为：10400，其中9200用户是第一天便已经在A中的用户，1200用户为当天新进组用户；第二天base_user为1200，第一天的次日留存为9200/10000=92%；
  • 第三天实验组A的用户数为：10200，其中8000用户为第一天便已经在A中的用户，1100用户为第二天进入A中的用户，1100为第三天进入A的用户；第三天的base_user为1100， 第一天的2日留存为8000/10000=80%， 第二天的次日留存为1100/1200=91.67%；
  • 然后分别把每个进入实验日期的指标用base_user进行加权平均，得到次日留存率、第2天留存率等。

如何计算「同期群留存趋势」每日每个实验版本的详细数据？
图片
示例如下：

日期

新进组人数

1天后

2天后

3天后

4天后

5天后

6天后

7天后

8天后

9天后

10天后

11天后

12天后

13天后

14天后

全部新进组用户

317907

4.99%

5.11%

5.24%

5.42%

5.58%

5.81%

6.11%

6.49%

6.93%

7.44%

8.48%

10.06%

13.77%

15.96%

20200715

24,230

20200714

23,941

1.60%

20200713

23,551

1.70%

1.70%

20200712

23,160

1.82%

1.85%

1.89%

20200711

22,725

1.74%

1.64%

1.70%

1.69%

20200710

22,391

1.79%

1.87%

1.73%

1.85%

1.76%

20200709

22,014

1.83%

1.91%

1.86%

1.93%

1.89%

1.84%

20200708

21,631

1.89%

1.83%

1.90%

1.75%

1.87%

1.76%

1.90%

20200707

21,237

1.93%

1.96%

1.87%

1.90%

1.86%

1.80%

1.91%

1.92%

20200706

20,857

1.97%

1.80%

1.87%

1.84%

1.86%

1.84%

1.78%

1.91%

1.90%

20200705

20,480

1.98%

1.98%

1.90%

2.01%

2.01%

2.02%

2.06%

2.03%

1.97%

1.91%

20200704

20,104

2.01%

2.04%

2.05%

2.05%

2.06%

2.20%

2.21%

2.23%

2.12%

1.88%

2.09%

20200703

19,813

2.44%

2.40%

2.47%

2.51%

2.27%

2.17%

2.17%

2.29%

2.24%

2.06%

2.04%

1.96%

20200702

27,373

30.55%

29.08%

27.47%

26.19%

24.61%

23.36%

21.84%

20.36%

18.99%

17.42%

16.04%

14.56%

13.16%

20200701

4,400

30.93%

29.73%

28.70%

27.48%

26.59%

25.32%

24.25%

23.23%

21.89%

20.77%

19.68%

18.57%

17.52%

15.95%

1天后：4.99%=（239411.60% + 235511.70% + 231601.82% + …+ 2737330.55% + 440030.93%）/（23941 + 23551 + … + 27373 + 4400） 4天后：5.42%=（227251.69% + 223911.85% + 220141.93% +… +2737326.19% + 440027.48%）/（22725 + 22391+…+27373 + 4400）

3.3 转化漏斗

详见：含转化漏斗的实验报告

四、高级分析

4.1 同期群分析

同期群分析 ：即将用户按初始行为的发生时间进行划分为群组（即同期群）

  • 对处于同期群的用户进行横向比较，从而得出相似群体随时间的变化，观察策略对用户整个生命周期的影响；
  • 对不同的同期群纵向比较，可以从总体上看到，应用的表现是否越来越好了，从而验证产品改进是否取得了效果。

详见：同期群分析

4.2 差异分析

在做完实验后，实验结果是针对所有实验的受众人群的，可以通过数据得到相应策略有正向效果/负向效果的结论。但是一个策略对于面向全部用户的正向/负向结论，并不等同于面对细分用户也有相同的结论。这时可以使用群体对比+差异分析，得到针对某一细分人群，实验策略为正向/负向的结论。
详见：差异分析

五. 置信度和置信区间

5.1 概念解读

置信度

  • 置信度（也称置信水平、置信系数、统计显著性），指实验组与对照组之间存在真正性能差异的概率，实验组和对照组之间衡量目标（即配置的指标）的差异不是因为随机而引起的概率。置信度使我们能够理解结果什么时候是正确的，对于大多数企业而言，一般来说，置信度高于95％都可以理解为实验结果是正确的。因此，默认情况下，「A/B测试」将置信水平参数值设置为95%。
  • 在A/B实验中，由于我们只能抽取流量做小样本实验。样本流量的分布与总体流量不会完全一致，这就导致没有一个实验结果可以100%准确——即使数据涨了，也可能仅仅由抽样误差造成，跟我们采取的策略无关。在统计学中，置信度的存在就是为了描述实验结果的可信度。

在实验的过程中，我们所抽取的样本流量实际上与总体流量会存在些许的差异，这些差异就决定了我们通过实验得出的结论或多或少会存在一些“误差”。

举个例子，实验中，我通过改变落地页的颜色让购买率提升了3%，但是因为样本流量并不能完全代表总体流量，有可能“我改变颜色这一策略其实没用，购买率提升3%是抽样结果导致的”。 那么发生这种“我的策略其实没用”事件的概率有多大呢？在统计学中，我们会用“显著性水平(α)”来描述发生这一事件的概率是多少。而置信度=1-α。 在「A/B测试」平台上，根据业界标准，显著性水平α取0.05。在A/B实验中，如果发生“我的策略其实没用”这一事件的概率小于0.05，我们即称实验结论已经“统计显著/可置信”。这意味着你采取的新策略大概率（A/B实验中意味着大于95%）是有效的。相反，如果这一事件的概率大于0.05，则称实验结论“不显著/不可置信”。

「A/B测试」主要采用假设检验来计算指标的置信度，实际上，要验证的是一对相互对立的假设：原假设和备择假设。

原假设（null hypothesis）：是实验者想要收集证据予以反对的假设。A/B实验中的原假设就是指“新策略没有效果”。 备择假设（alternative hypothesis）：是实验者想要收集证据予以支持的假设，与原假设互斥。A/B实验中的备择假设就是指“新策略有效果”。

利用反证法来检验假设，意味着我们要利用现有的数据，通过一系列方法证明原假设是错误的（伪），并借此证明备择假设是正确的（真）。这一套方法在统计学上被称作原假设显著性检验。
置信区间
主要通过某个指标或留存的实验版本均值变化值以及置信区间来判断，在当前指标或用户留存上，实验版本是否比对照版本表现得更好。

  • 如果在95%置信度下，置信区间同为正或者同为负，说明实验结果是统计显著的。
  • 如果在95%置信度下，置信区间为一正一负，说明实验结果是非统计显著的。

5.2 示例

统计正向显著
如下图所示，表明实验版本样本均值对比对照版本的变化率为+46.822%。在95%置信度下，置信区间为[46.589%，47.055%]，统计显著正向，说明当前的样本容量条件下已经检测出实验版本优于对照版本。
图片
统计负向显著
如下图所示，表明实验版本样本均值对比对照版本的变化率为-26.553%。在95%置信度下，置信区间为[-26.786%，-26.320%]，统计显著负向，说明当前的样本容量条件下已经检测出实验版本在核心指标上劣于对照版本。
图片
不显著
如下图所示，表明实验版本样本均值对比对照版本的变化率为-0.941%。在95%置信度下，置信区间为[-3.552%，1.670%]，置信区间一负一正，实验结果是非统计显著的。
图片

六、下载进组用户ID
  • 在实验报告页中，点击原有的进组人数可以直接下载所有进组用户ID和对应的分组信息，包含用户id、实验名称、实验分组、过滤条件（如有）信息；
  • 最多可以下载500万条数据

图片