1.1 定基法
1.1.1 概述
定基法,全称定基替代法,是用于解决变化分解问题的算法。 其核心思想是,假设其他维值保持不变,只有一个维值发生变化,这时给总指标带来的变化,就是这个维值的贡献。
下面展示不同类型指标下,定基法的详细计算方法。
1.1.2 算法配置
(1)适用范围
假设数据集表为
a_int | b_int | c_int | d_string |
|---|---|---|---|
1 | 2 | 3 | “啊啊啊” |
4 | 5 | 6 | “哈哈哈” |
(2)直接表达式配置
核心指标 | 聚合方式 |
|---|---|
a_int | 求和 |
a_int + b_int | 求和 |
case when a_int > 10 then 1 else 0 end | 计数 |
d_string | 计数不同 |
(3)加法配置
核心指标 | 聚合方式 |
|---|---|
sum(a_int) | 聚合 |
sum(a_int) + sum(b_int) | 聚合 |
sum(a_int) + sum(case when a_int > 10 then 1 else 0 end) | 聚合 |
sum(a_int) + count(b_int) | 聚合 |
sum(a_int) + 100 | 聚合 |
count(distinct a_int) - count(a_int) | 聚合 |
(4)除法配置
核心指标 | 聚合方式 |
|---|---|
sum(a_int) / sum(b_int) | 聚合 |
sum(a_int) / count(b_int) | 聚合 |
sum(a_int) / count(distinct b_int) | 聚合 |
( sum(a_int) + sum(b_int) ) / count(c_int) | 聚合 |
count(distinct a_int) / count(a_int) | 聚合 |
avg(a_int) | 聚合 |
avg(a_int) 可以视为 sum(a_int)/count(a_int)
(5)其他复杂类型配置
核心指标 | 聚合方式 |
|---|---|
sum(a_int) + ( sum(b_int) / count(c_int) ) | 聚合 |
( sum(a_int) * sum(b_int) ) / count(c_int) | 聚合 |
( sum(a_int) * sum(b_int) ) / ( count(c_int) * count(c_int) ) | 聚合 |
sum(a_int) / sum(b_int) + sum(a_int) / count(b_int) | 聚合 |
avg(a_int) - avg(b_int) | 聚合 |
1.1.3 加法指标的算法说明(原Delta法)
(1)计算方法
维度项变化值在父层级变化值的占比
(2)解读
- 第一行 维度A:AA,贡献率= 4021/3483 = 115.45%
- 第二行 是否为B:0,贡献率=3880/3483 = 111.40%
- 第十行 是否为B:1,贡献率=-397/3483 =-11.40%
其中维度[是否为B]只有2个值,也可以看到它的贡献率总和=111.40%-11.40%=100%
在Delta法中,如果大盘DNU下跌了,则同向因子是下降的维度值,反向因子是上升的维度值。
同向影响因子:对大盘指标同向变动做出贡献的因子,贡献率为正的因子会判定为同向影响因子。
反向影响因子:对大盘指标反向变动做出贡献的因子,贡献率为负的因子会判定为反向影响因子。
1.1.4 除法指标的算法说明
审核准确率指标,是一个复杂的除法复合指标。 满意度=满意量/参评量。
其中分子和分母是可加和的,如:满意量=处理组A的满意量+处理组B的满意量+……+处理组N的满意量
(1)计算方法
使用今天的维度值指标代替昨天的维度值指标,得到与昨天大盘的差值。
附: 定基法的计算公式与Bhagwan, R., Kumar, R., Ramjee, R., Varghese, G., Mohapatra, S., Manoharan, H., & Shah, P. (2014). Adtributor: Revenue Debugging in Advertising Systems (pp. 43–55). 里对EP值的计算公式一致。该方法是通过偏分差值来作为衡量指标,论文链接:Adtributor: Revenue Debugging in Advertising Systems
(2)例子
- 分子变化情况
维度项 | 基础期分子 | 基础期分母 | 基础期指标 | 对比期分子 | 对比期分母 | 对比期指标 | EP |
|---|---|---|---|---|---|---|---|
A | 10 | 10 | 1 | 5 | 10 | 0.5 | -0.166666667 |
B | 1 | 10 | 0.1 | 10 | 10 | 1 | 0.3 |
C | 19 | 10 | 1.9 | 19 | 10 | 1.9 | 0 |
总 | 30 | 30 | 1 | 34 | 30 | 1.133333333 | 0.133333333 |
- 分母变化情况
维度项 | 基础期分子 | 基础期分母 | 基础期指标 | 对比期分子 | 对比期分母 | 对比期指标 | EP |
|---|---|---|---|---|---|---|---|
A | 10 | 10 | 1 | 10 | 50 | 0.2 | -0.571428571 |
B | 1 | 10 | 0.1 | 1 | 2 | 0.5 | 0.363636364 |
C | 19 | 10 | 1.9 | 19 | 10 | 1.9 | 0 |
总 | 30 | 30 | 1 | 30 | 62 | 0.483870968 | -0.516129032 |
- 分子分母都变化情况
维度项 | 基础期分子 | 基础期分母 | 基础期指标 | 对比期分子 | 对比期分母 | 对比期指标 | EP |
|---|---|---|---|---|---|---|---|
A | 10 | 10 | 1 | 5 | 60 | 0.083333333 | -0.6875 |
B | 1 | 10 | 0.1 | 10 | 100 | 0.1 | -0.675 |
C | 19 | 10 | 1.9 | 19 | 10 | 1.9 | 0 |
总 | 30 | 30 | 1 | 34 | 170 | 0.2 | -0.8 |
(3)解读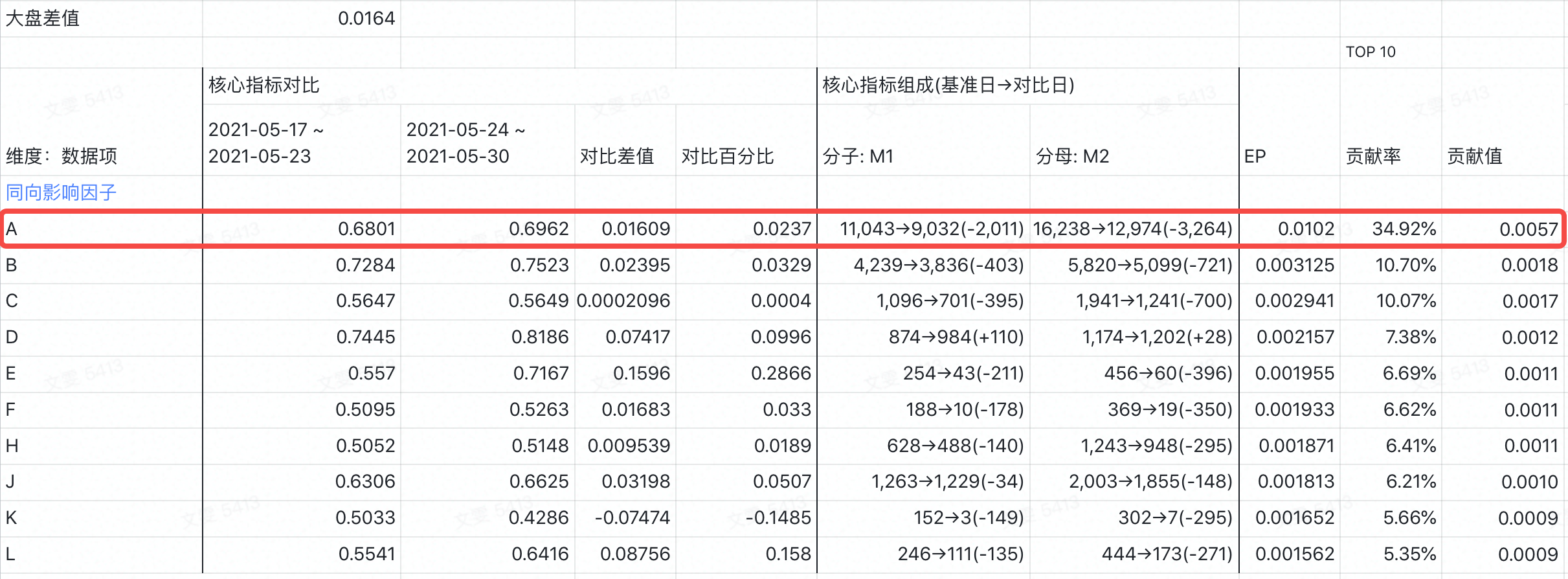
以维度值A为例,解释如何计算得到的EP和贡献率:
EP= (30461-11043+9032)/(41423-16238+12974)-30461/41423=0.0102,其中30461是基准周05-17~05-23的大盘分子,41423是基准周05-17~05-23的大盘分母
贡献率:0.0102/所有的维度值的EP=34.92%,即维度值A对大盘变动的贡献是34.92%。
贡献值:贡献率*大盘差值=34.92%*0.0164=0.0057,即维度值A对大盘差值变动贡献了0.0057。
注:分母是所有的维度值的EP。
1.1.5 组合指标的算法说明
组合指标,即指标由多个基础指标组合运算得到。这时需要使用 差分法 计算维值对组合指标带来的变化。
设f、g、h为基础指标在基期的值,Delta{f}、Delta{g}、Delta{h} 为某维值给基础指标带来的变化,a、b、c 为常数,则该维值对组合指标带来的变化,可通过在组合公式上使用差分法得到: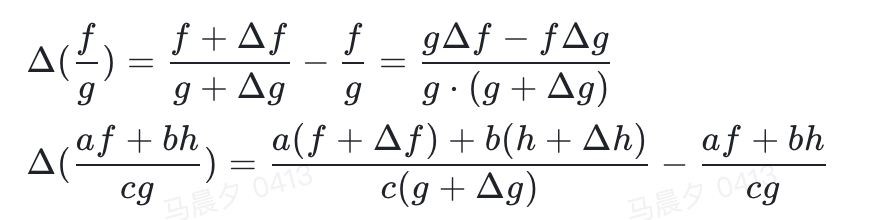
如,指标:点击率 = 点击量 / 曝光量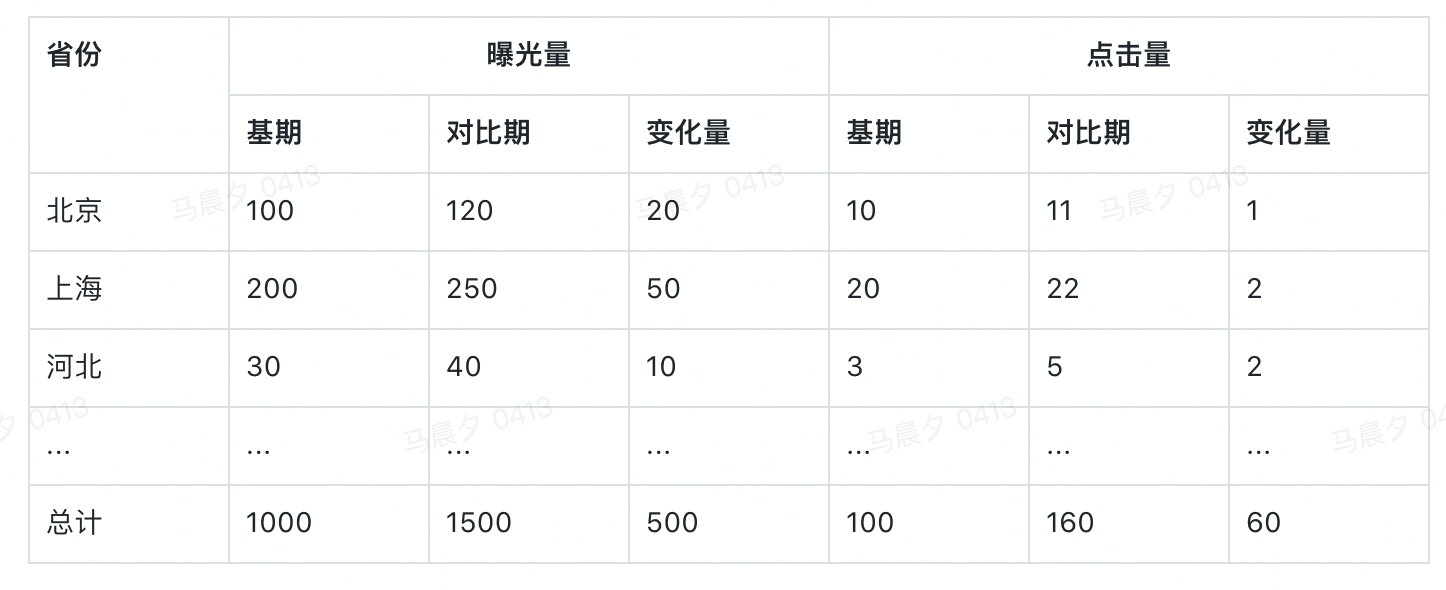
北京对总点击率的贡献值是: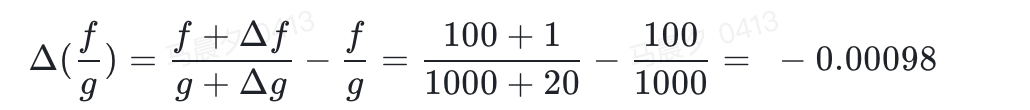
在所有维值上对贡献值进行归一化,即可得到贡献率: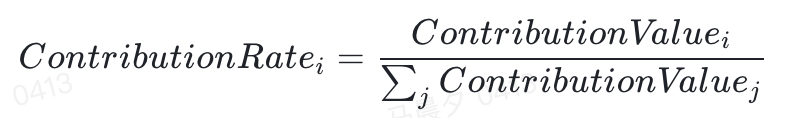
这种方法对指标的计算公式没有限制,任意公式均可使用。
1.2 综合贡献法-比率类维度分析
(1)适用范围
满意度指标,是一个分子分母可加和的除法复合指标。 满意度=满意量/参评量
其中分子和分母是可加和的,如:参评量=处理组A的参评量+处理组B的参评量+……+处理组N的参评量
(2)计算方法
综合贡献法从种类内和种类间两个角度分别计算变动的贡献值。
- 种类内变化回答的是:该处理组满意度变化相比满意度不变对大盘整体产生的影响
- 种类间变化回答的是:该处理组参评量占比变化相比不变化对大盘整体产生的影响
计算:
- 某处理组基准日参评量(分母)占比为w1,对比日参评量(分母)占比为w2;基准日满意度为q1,对比日满意度为q2;基准日大盘满意度为Q1,对比日大盘满意度为Q2。
- 种类内贡献值=w2*(q2-q1)=对比日参评量占比*(该处理组对比日的满意度-该处理组基准日的满意度)=对比日的占比* 核心指标的变动
- 种类间贡献值=(q1-Q1)* (w2-w1)=(该处理基准日满意度-大盘满意度)* (对比日参评量占比-基准日参评量占比)=基准日与大盘的差值* 分母占比变动
- 总计综合贡献值=大盘核心指标变动差值
(3)解读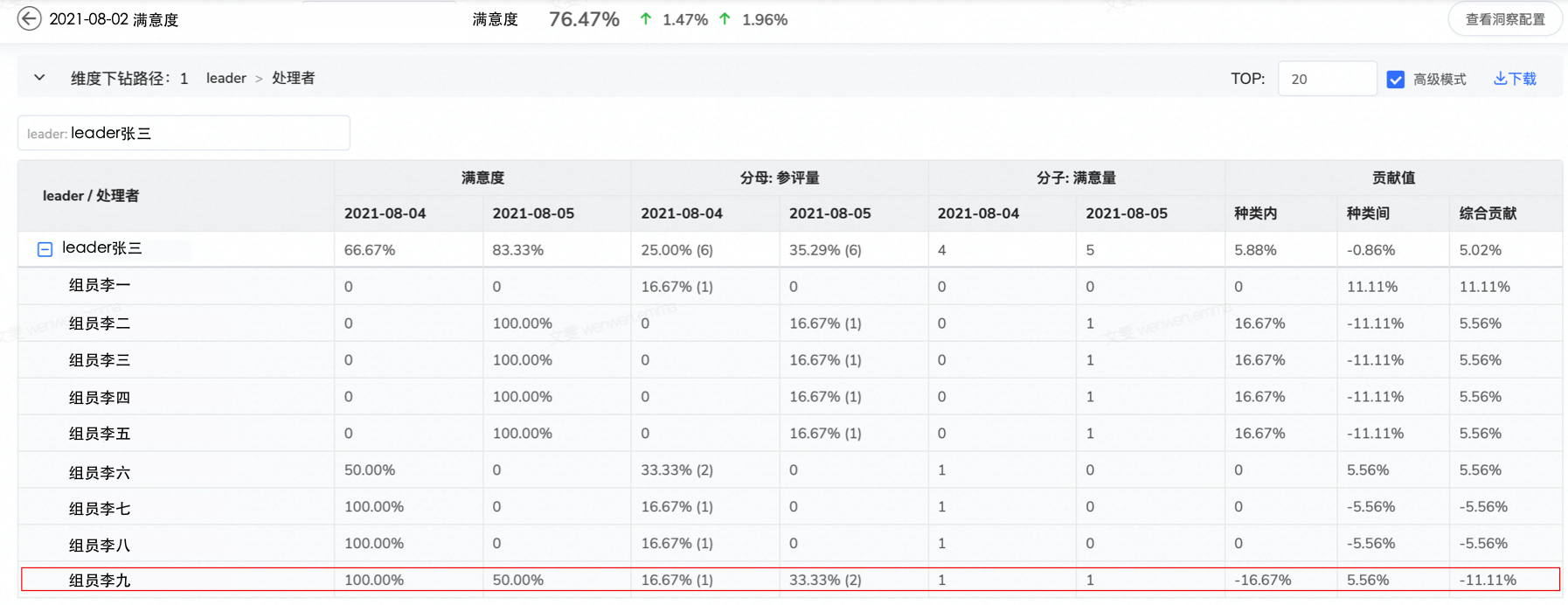
计算说明
以组员李九为例,解释如何计算得到的种类内贡献值,种类间贡献值
- 种类内贡献值=w2*(q2-q1)=33.33%*(50.00%-100.00%)=-16.67%
- 种类间贡献值=(q1-Q1)* (w2-w1)=(100.00%-66.67%)*(33.33%-16.67%)=5.56%,其中Q1(66.67%)是父节点leader张三基准日的满意度
- 综合贡献值=种类内贡献值+种类间贡献值=-16.67%+5.56%=-11.11%
组员李九对leader张三的满意度差值16.66%贡献了值-11.11%。
注意: 在层级分析中,子维度下所有值的综合贡献值总计=父维度核心指标变动差值。在上例中,1)处理者下面所有的值组员李一到李九,它们的综合贡献值总计=16.66%=leader张三的满意度差值
数据解读
- leader张三,种类内贡献值=5.88%,种类间贡献值=-0.86%,综合贡献值=5.02%。大盘满意度上升了1.47%,其中leader张三贡献了值5.02%。对leader张三来说,主要变化是自身能力(满意度)提高了5.88%。
- 组员李一,种类内贡献值=0,种类间贡献值=11.11%,综合贡献值=11.11%。leader张三满意度上升了16.66%,其中组员李一贡献了值11.11%。组员种类内贡献为0,主要变化是结构(参评量占比)。
2.1 根因定位原因
当根因与某维度无关时,该维度下的维值依然会产生贡献率,且贡献率与维值占比成正比。 因此用户需要从众多维度中定位到哪些维度是根因,进而考虑这些维度的维度项的贡献率。 本产品支持利用JS散度 来定位根因。目前应用在使用了定基法的维度归因报告的总结中。该算法会从指定的多条维度下钻路径中定位到根因所在维度,并结合贡献率进一步提炼出根因维度项。
2.2 计算方法
相对熵用来衡量当前维度在基准期和对比期两个分布之间的差异,如果分布保持不变,说明根因与该维度变量无关、独立 ;如果分布变化大,说明根因与该维度相关性大。
- 相对熵(JS散度) 的计算公式为
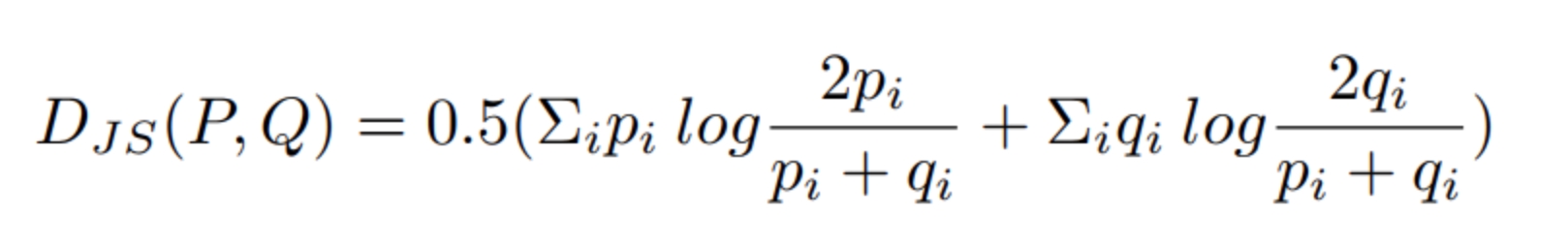
- 相对熵介于0~1之间,数值越大表示根因的可能性越大。